Solution
Gievn the equation below
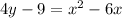
To find the vertex and focus of the given equation, we apply the parabola standard equation which is
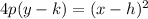
Where p is the focal length and the vertex is (h,k)
Rewriting the equation in standard form gives
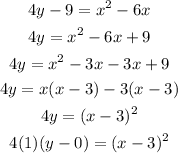
Relating the parabola standard equation with the given equation, the vertex of the parabola is
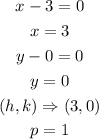
Hence, the vertex is (3,0)
The focus of the parabola formula is
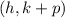
Where
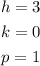
Substitute the values of h, k and p into the focus formula
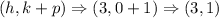
Hence, the focus is (3, 1)