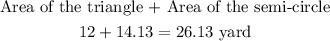The shape in question is a composite shape.
It comprises two(2) shapes which are a triangle and a semi-circle.
The area of the shape is the sum of the area of the triangle and that of the semi-circle
The area of the triangle is:

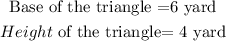
Thus,
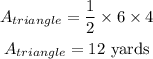
Area of the Semi-circle is:
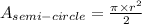
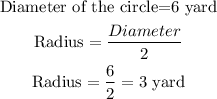
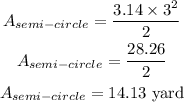
Hence, the area of the composite shape is: