Question

I need help Options for the first box: -3, 1/3, 3, -1/3 Options for the second box -303, 363, 183, -60

Answer 1

To find the common ratio of the sequence, divide each of the elements of the sequence by the element that precedes it:

`\begin{gathered} (-9)/(3)=-3 \\ (27)/(-9)=-3 \\ (-81)/(27)=-3 \end{gathered}`

Since the quotient is always -3, then the common ratio is equal to -3.

To find the fifth term of the sequence, multiply the fourth term, which is -81, times -3:

`-81*-3=243`

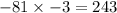
Once that we know the first five terms of the sequence, add them to find their sum:

`\begin{gathered} 3-9+27-81+243 \\ =-6+27-81+243 \\ =21-81+243 \\ =-60+243 \\ =183 \end{gathered}`

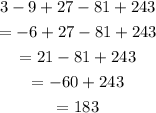
Therefore:

The common ratio of the sequence is -3.

The sum of the first five terms of the sequence is 183.