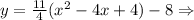Question

Write the equation for the quadratic function in vertex form & standard form with the given vertex that passes through the given point.Vertex (2, -8) through the point (4, 3)

Answer 1

We will have the following:

`\begin{gathered} y=a(x-2)^2-8\Rightarrow3=a(4-2)^2-8 \\ \\ \Rightarrow3=4a-8\Rightarrow4a=11 \\ \\ \Rightarrow a=(11)/(4) \end{gathered}`

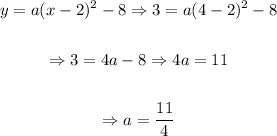
So, the equation in vertex form is:

`y=(11)/(4)(x-2)^2-8`

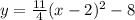
And in standard form:

`\begin{gathered} y=(11)/(4)(x^2-4x+4)-8\Rightarrow y=(11)/(4)x^2-11x+11-8 \\ \\ \Rightarrow y=(11)/(4)x^2-11x+3 \end{gathered}`

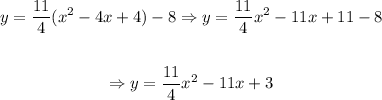
***Explanation***

We know that the quadratic expression in vertex form follows:

`y=a(x-h)^2+k`

Where (h, k) is the vertex of the expression. Now, we know that the vertex is (2, -8), so we replace those values and we obtain:

`y=a(x-2)^2+(-8)\Rightarrow y=a(x-2)^2-8`

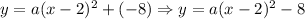
Now, in order to determine "a" we must replace one point (That is not the vertex) in the expression and solve for "a", and we are told that the point (4, 3) is in one of the solutions, so:

`\begin{gathered} 3=a(4-2)^2-8\Rightarrow3=a(2)^2-8 \\ \\ \Rightarrow11=4a\Rightarrow a=(11)/(4) \end{gathered}`

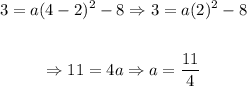
Thus, the expression in vertex form is then:

`y=(11)/(4)(x-2)^2-8`

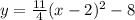
And to determine the standard form, we simply expand the equation in vertex form:

`y=(11)/(4)(x^2-4x+4)-8\Rightarrow`