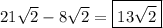Hello!
To solve this exercise, we must simplify these square roots until we have the same square root in both numbers (by the factorization process):

First, let's factorize the square root of 98:
So, we know that:
![\begin{gathered} 3√(98)=3√(7^2*2)=3\sqrt[\cancel{2}]{7\cancel{^2}*2}=3*7√(2)=21√(2) \\ \\ 3√(98)=21√(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fmh1xnjf3cm4b0spoirr9b08sgh770ybpu.png)
Now, let's do the same with the square root of 128:
So:
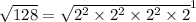
Notice that it also could be written as:
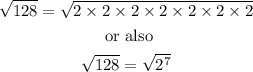
As we are talking about square roots, it will be easier if we group them in pairs of powers of 2, as I did:
![\sqrt[2]{128}=\sqrt[2]{2^2*2^2*2^2*2^1}](https://img.qammunity.org/2023/formulas/mathematics/college/g4vo27t0oqphtt7a3cgoe6cuko359dhvwh.png)
Now, let's analyze it:
If the number inside the root has exponent 2, we can cancel this exponent and remove the number inside the root. Then, we can write it outside of the root, look:
![\begin{gathered} \sqrt[2]{128}=\sqrt[2]{2^{\cancel{2}}*2^{\cancel{2}}*2^{\cancel{2}}*2^1} \\ \sqrt[2]{128}=2*2*2\sqrt[2]{2^1} \\ \sqrt[2]{128}=8\sqrt[2]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3ad0t13hgnip53jw5ou9k5gjpezqtycfgi.png)
Now, let's go back to the exercise:
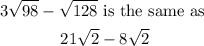
So, we just have to solve it now: