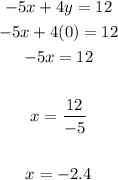Question

Graph the solution to the following system of inequalities. Don’t forget to answer the point in the solution set.

Answer 1

Given the following System of Inequalities:

`\begin{cases}7x+4y<16 \\ -5x+4y\ge12\end{cases}`

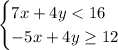
You need to remember that the Slope-Intercept form of the equation of a line is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

The steps to graph the System of Inequalities are:

1. In this case, you know that the first line is:

`7x+4y=16`

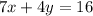
So you need to solve for "y" in order to write it in Slope-Intercept form:

`\begin{gathered} 4y=-7x+16 \\ \\ y=(-7)/(4)x+(16)/(4) \\ \\ y=-(7)/(4)x+4 \end{gathered}`

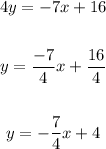
You can identify that the y-intercept is:

`b_1=4`

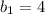
2. Since the value of "y" is zero when the line intersects the x-axis, you can substitute that value into the equation and solve for "x", in order to find the x-intercept:

`\begin{gathered} 7x+4y=16 \\ 7x+4(0)=16 \\ 7x=16 \\ \\ x=(16)/(7)\approx2.286 \end{gathered}`

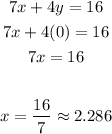
3. Now you know that the first line passes through these points:

`(0,4);(2.286,0)`

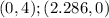
4. The second line is:

`-5x+4y=12`

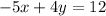
So you can solve for "y" in order to write it in Slope-Intercept form:

`\begin{gathered} 4y=5x+12 \\ \\ y=(5)/(4)x+(12)/(4) \\ \\ y=(5)/(4)x+3 \end{gathered}`

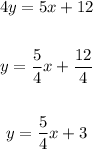
Notice that the y-intercept is:

`b_2=3`

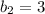
5. Knowing that "y" is zero when the line intersects the x-axis, you can substitute that value into the equation of the second line and solve for "x" to find the x-intercept:

`\begin{gathered} -5x+4y=12 \\ -5x+4(0)=12 \\ -5x=12 \\ \\ x=(12)/(-5) \\ \\ x=-2.4 \end{gathered}`