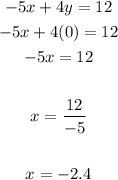Given the following System of Inequalities:
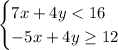
You need to remember that the Slope-Intercept form of the equation of a line is:

Where "m" is the slope and "b" is the y-intercept.
The steps to graph the System of Inequalities are:
1. In this case, you know that the first line is:
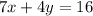
So you need to solve for "y" in order to write it in Slope-Intercept form:
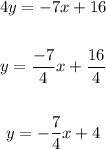
You can identify that the y-intercept is:
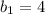
2. Since the value of "y" is zero when the line intersects the x-axis, you can substitute that value into the equation and solve for "x", in order to find the x-intercept:
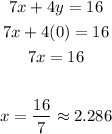
3. Now you know that the first line passes through these points:
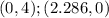
4. The second line is:
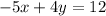
So you can solve for "y" in order to write it in Slope-Intercept form:

Notice that the y-intercept is:
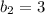
5. Knowing that "y" is zero when the line intersects the x-axis, you can substitute that value into the equation of the second line and solve for "x" to find the x-intercept: