Answer
Domain is all real numbers except x ≠ 0, -4, and 4
Vertical asymptote at x = 0, -4, and 4
Step-by-step explanation
Given function:
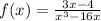
Note: The domain of a function is a set of input or argument values for which the function is real and defined.
For the function to be real; the denominator must not be equal zero, i.e.
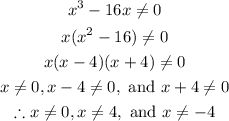
Hence, the domain is all real numbers except x ≠ 0, -4, and 4.
Note: A vertical asymptote with a rational function occurs when there is division by zero.
Hence, the vertical asymptote at x = 0, -4, and 4