Question

Identify the domain, vertical asymptotes and horizontal asymptotes of the following rational function: f(x)= \frac{3x-4}{x^3-16x} Domain is all real numbers except x\\eq Answer , Answer and AnswerVertical asymptote at x= Answer , Answer and AnswerHorizontal asymptote at y= Answer

Answer 1

Domain is all real numbers except x ≠ 0, -4, and 4

Vertical asymptote at x = 0, -4, and 4

Step-by-step explanation

Given function:

`f(x)=(3x-4)/(x^3-16x)`

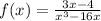
Note: The domain of a function is a set of input or argument values for which the function is real and defined.

For the function to be real; the denominator must not be equal zero, i.e.

`\begin{gathered} x^3-16x\\e0 \\ x(x^2-16)\\e0 \\ x(x-4)(x+4)\\e0 \\ x\\e0,x-4\\e0,\text{ and }x+4\\e0 \\ \therefore x\\e0,x\\e4,\text{ and }x\\e-4 \end{gathered}`

Hence, the domain is all real numbers except x ≠ 0, -4, and 4.

Note: A vertical asymptote with a rational function occurs when there is division by zero.

Hence, the vertical asymptote at x = 0, -4, and 4