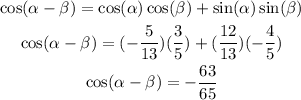To solve the problem, we will make use of the identity:
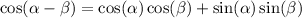
ANGLE α
The angle lies in the second quadrant. The only positive ratio is the sine.
If we have that:
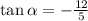
Displaying this on a triangle for ease of working, we have:
Therefore, the length of the hypotenuse will be:
![\begin{gathered} x=\sqrt[]{12^2+5^2}=\sqrt[]{144+25}=\sqrt[]{169} \\ x=13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/thz39opt96qo6uw80mspqy27xdwi806ef8.png)
Therefore, we have that:

ANGLE β
This angle lies in the fourth quadrant. Only the cosine ratio is positive in this quadrant.
We are given in the question:
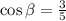
Displaying this on a triangle for ease of working, we have:
Therefore, using the Pythagorean Triplets, we have that:
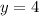
Therefore, we have that:
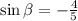
SOLVING THE IDENTITY
Applying the identity quoted earlier, we have: