Answer:
7 units
Explanation:
Forming an equation:
There is a one-time signup fee. Let that be represented by "a".
Then, there's also a weekly fee. Let that be represented by "b", i.e., the fee for one week is "b" units.
==> If she goes to the gym for x weeks, then her total weekly fee will be "b" times "x" units.
If we represent her total cost after membership by "y", our equation becomes:
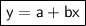
We're provided with three values of x and y.
- When x = 6, y = 133
- When x = 12, y = 175
- When x = 24, y = 259
The solution to the equation:
Substitute the respective values of x and y into the equation.
#1
133 = a + 6b
==> a = 133 - 6b
#2
175 = a + 12b
Since we only need the values of two variables we'll use only two equations.
Substituting from #1 for a:
175 = (133 - 6b) + 12b
==> 175 = 133 + 6b
==> 175 - 133 = 6b
==> 42 = 6b
==> b = 7
And b is the amount she pays each week.
So, the answer is 7 units.