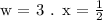Question

Find the values of w and x that makeup NOPQ a parallelogram. A. W = 1/2 X = 1/2 B. W = 3 X = 2 C. W = 2 X = 2 D. W = 3 X = 1/2 Please select the best answer from the choices Provided

Answer 1

Step 1:

Properties of Parallelograms Explained

1. Opposite sides are parallel. ...

2. Opposite sides are congruent. ...

3. Opposite angles are congruent. ...

4. Same-Side interior angles (consecutive angles) are supplementary. ...

5. Each diagonal of a parallelogram separates it into two congruent triangles. ...

6. The diagonals of a parallelogram bisect each other.

Step 2:

The diagonals of a parallelogram bisect each other.

`\begin{gathered} The\text{ }diagonals\text{ }of\text{ }a\text{ }parallelogram\text{ }bisect\text{ }each\text{ }other. \\ w\text{ + 7 = 5w - 5} \\ and \\ (3)/(2x)\text{ = 3} \end{gathered}`

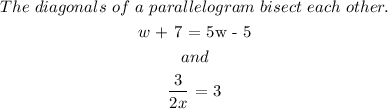
Step 3

`\begin{gathered} Solve\text{ for w:} \\ w\text{ + 7 = 5w - 5} \\ Add\text{ similar terms} \\ 7\text{ + 5 = 5w - w} \\ 12\text{ = 4w} \\ w\text{ = }(12)/(4) \\ w\text{ = 3} \end{gathered}`

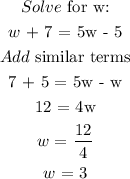
Step 4

`\begin{gathered} Solve\text{ for x:} \\ (3)/(2x)\text{ = 3} \\ 3*2x\text{ = 3} \\ \\ 6x\text{ = 3} \\ \\ x\text{ = }(3)/(6) \\ \\ x\text{ = }(1)/(2) \end{gathered}`

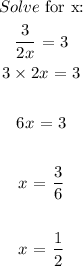
Final answer

`\text{w = 3 . x = }(1)/(2)`