Question

ABCD is a rectangle. Find the coordinates of P, the midpoint of AC. [B is (18,12) ]

Answer 1

the coordinates of P is (9, 6)

Step-by-step explanation:

Coordinate of B = (18, 12)

In a rectangle, the opposite parallal sides are equal

AB = DC

AD = BC

We need to find the coordinates of A and C inoder to get P:

Since the x coordinate of B is 18, the x coordinate of C will also be 18

C is on the y axis, this means its y coordinate will be zero

Coordinate of C (x, y) becomes: (18, 0)

The y coordinate of B is 12, the y coordinate of A will also be 12

A is on the y axis. This means the x coordinate of A will be zero

Coordinate of A (x, y becomes): (0, 12)

To get P, we will apply the midpoint formula:

`\text{Midpoint = }(1)/(2)(x_1+x_2),\text{ }(1)/(2)(y_1+y_2)`

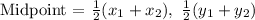
Using the points A (0, 12) and C (18, 0) to get coordinates of P:

`\begin{gathered} x_1=0,y_1=12,x_2=18,y_2\text{ = 0} \\ \text{midpoint = }(1)/(2)(0+18),\text{ }(1)/(2)(12+0) \\ \text{midpoint = }(1)/(2)(18),\text{ }(1)/(2)(12) \\ \text{midpoint = (9, 6)} \end{gathered}`

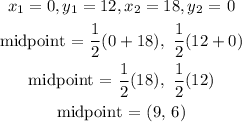
Hence, the coordinates of P is (9, 6)