the coordinates of P is (9, 6)
Step-by-step explanation:
Coordinate of B = (18, 12)
In a rectangle, the opposite parallal sides are equal
AB = DC
AD = BC
We need to find the coordinates of A and C inoder to get P:
Since the x coordinate of B is 18, the x coordinate of C will also be 18
C is on the y axis, this means its y coordinate will be zero
Coordinate of C (x, y) becomes: (18, 0)
The y coordinate of B is 12, the y coordinate of A will also be 12
A is on the y axis. This means the x coordinate of A will be zero
Coordinate of A (x, y becomes): (0, 12)
To get P, we will apply the midpoint formula:
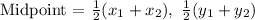
Using the points A (0, 12) and C (18, 0) to get coordinates of P:

Hence, the coordinates of P is (9, 6)