Solution
- The question gives us a composite figure made up of a cylinder and a cube.
- We are required to find the volume of the cylinder and the cube and then use the results to find the volume of the composite figure.
- The formulas needed for this calculation are:

- With the information above, we can proceed to solve the question
Volume of the Cylinder:
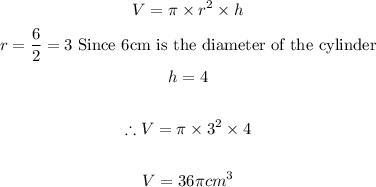
Volume of Cube:
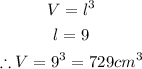
Volume of Composite Figure:
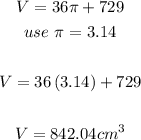
Final Answer
The volume of the composite shape is 842.04 cm³