Step 1: Represent a with an unknown
Let a number be x
Step 2: Represent the given information with an equation
From the first statement, the sum of a number and seven is tripled can be represented with the equation below:

The second statement reflects that the result of the first statement is eight times a number. Eight times a number is
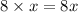
The result of the first statement and the second statement is

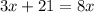
Step 3: Solve for the unknown
The solution of the unknown is as shown below:
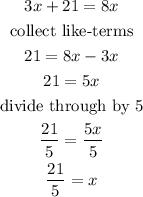
![\begin{gathered} (21)/(5)=x \\ x=(21)/(5) \\ \operatorname{Re}-\text{write as a mixed fraction} \\ x=4(1)/(5) \end{gathered}]()
Hence, the number is 4 1/5