Factoring
Factor the expression:
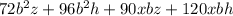
Divide the expression into two halves:
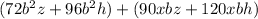
Factor b^2 from the first group and xb from the second group:
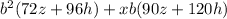
Now find the greatest common multiple of 72 and 96:
72= 2*2*2*3*3
96=2*2*2*2*2*2*3
Now we take the common factors with their least number of repetitions:
GCF=2*2*2*3=24
Now we find the GCF of 90 and 120:
90=2*3*3*5
120=2*2*2*3*5
GCF=2*3*5=30
Taking the GCF of each group:
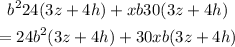
Now we finally take out 3z+4h from both groups:
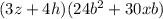
This last expression can be further factored by taking out 6b from both terms:
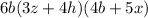
This is the final expression factored as much as possible