Question

72bz +96b2h + 90xbz + 120xbh +

Answer 1

Factoring

Factor the expression:

`72b^2z+96b^2h+90xbz+120xbh`

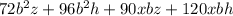
Divide the expression into two halves:

`(72b^2z+96b^2h)+(90xbz+120xbh)`

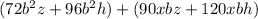
Factor b^2 from the first group and xb from the second group:

`b^2(72z+96h)+xb(90z+120h)`

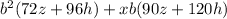
Now find the greatest common multiple of 72 and 96:

72= 2*2*2*3*3

96=2*2*2*2*2*2*3

Now we take the common factors with their least number of repetitions:

GCF=2*2*2*3=24

Now we find the GCF of 90 and 120:

90=2*3*3*5

120=2*2*2*3*5

GCF=2*3*5=30

Taking the GCF of each group:

`\begin{gathered} b^224(3z+4h)+xb30(3z+4h) \\ =24b^2(3z+4h)+30xb(3z+4h) \end{gathered}`

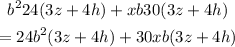
Now we finally take out 3z+4h from both groups:

`\mleft(3z+4h\mright)(24b^2+30xb)`

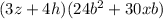
This last expression can be further factored by taking out 6b from both terms:

`6b(3z+4h)(4b+5x)`

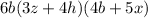
This is the final expression factored as much as possible