Question

I need help with his practice problems from my ACT prep guidePlease show your work in steps

Answer 1

`-\sqrt[]{6}+1`

Step-by-step explanation:

Given the below expression;

`(\tan(-(2\pi)/(3)))/(\sin((7\pi)/(4)))-\sec (-\pi)`

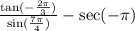
Recall that;

`\begin{gathered} \sec x=(1)/(\cos x) \\ \sin x=\cos ((\pi)/(2)-x) \end{gathered}`

So we can rewrite the expression as;

`\begin{gathered} (\tan(-(2\pi)/(3)))/(\cos(\pi-(7\pi)/(4)))-(1)/(\cos(-\pi)) \\ (\tan(-(2\pi)/(3)))/(\cos(-(5\pi)/(4)))-(1)/(\cos(-\pi)) \end{gathered}`

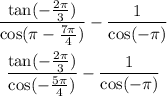
Also, recall that;

`\begin{gathered} \cos (-x)=\cos x \\ \tan (-x)=-\tan x \end{gathered}`

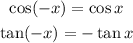
So we'll have;

`(-\tan ((2\pi)/(3)))/(\cos ((5\pi)/(4)))-(1)/(\cos (\pi))`

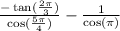
From the Unit circle, we have that;

`\begin{gathered} \cos \pi=-1 \\ \cos ((5\pi)/(4))=\frac{-\sqrt[]{2}}{2} \\ \tan ((2\pi)/(3))=-\sqrt[]{3} \end{gathered}`

Substituting the above values into the expression and simplifying, we'll have;

`\begin{gathered} \frac{-(-\sqrt[]{3})}{\frac{-\sqrt[]{2}}{2}}-(1)/(-1)=\frac{\sqrt[]{3}}{\frac{-\sqrt[]{2}}{2}}+1=-\frac{2\sqrt[]{3}\sqrt[]{2}}{\sqrt[]{2}\cdot\sqrt[]{2}}+1 \\ =-\sqrt[]{6}+1 \end{gathered}`