Answer:
![-\sqrt[]{6}+1](https://img.qammunity.org/2023/formulas/mathematics/college/ajhi3410jtsxtp28mnac1jz0fdgl7kgny2.png)
Step-by-step explanation:
Given the below expression;
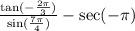
Recall that;
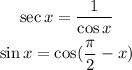
So we can rewrite the expression as;
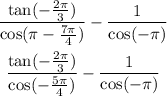
Also, recall that;
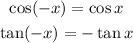
So we'll have;
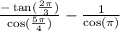
From the Unit circle, we have that;
![\begin{gathered} \cos \pi=-1 \\ \cos ((5\pi)/(4))=\frac{-\sqrt[]{2}}{2} \\ \tan ((2\pi)/(3))=-\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/chc225vi9piv31bipzjimoh55o36h7pnod.png)
Substituting the above values into the expression and simplifying, we'll have;
![\begin{gathered} \frac{-(-\sqrt[]{3})}{\frac{-\sqrt[]{2}}{2}}-(1)/(-1)=\frac{\sqrt[]{3}}{\frac{-\sqrt[]{2}}{2}}+1=-\frac{2\sqrt[]{3}\sqrt[]{2}}{\sqrt[]{2}\cdot\sqrt[]{2}}+1 \\ =-\sqrt[]{6}+1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/czj8yuqqe5m6vmbj9ti7qbj08yv3l45jd4.png)