Rewrite each equation in slope intercept form . Then determine whether the lines are perpendicular . Explain your answer .. y - 6 = - 5/2 (x + 4) 5y = 2x + 6

Question

asked Dec 22, 2023 15.6k views

1 Answer

Mark Giblin · Answer 1 · 2023-12-26T15:34:29+0000

y - 6 = - 5/2 (x + 4)

To write in slope-intercept form means to write in the form;

y= mx + b

where m is the slope and b is the intercept

y - 6 = - 5/2 (x + 4)

open the parenthesis

y - 6 = -5/2 x - 10

add 6 to both-side of the equation

y = - 5/2 x - 10 + 6

y = -5/2 x - 4

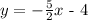
$y=-(5)/(2)x\text{ - 4}$

Next is to check whether 5y = 2x + 6 is perpendicular to the above

To do that, we have to make the equation to be in the form y=mx+ b

5y = 2x + 6

Divid through by 5

y = 2/5 x + 6/5

$y\text{ = }(2)/(5)x\text{ + }(6)/(5)$

The slope of perpendicular equation, when multiply gives minus one (-1)

The slope of the first equation = -5/2

The slope of the second equation is 2/5

Multiplying the two slopes;

(-5/2) (2/5) = -1

Hence the lines are perpendicular