Question

Use appropriate identities to rewrite the following expression in terms containing only first powers ofsine.4tanx1 + tan2x

Answer 1

The given question is

`(4\tan x)/(1+\tan ^2x)`

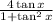
Use the identity

`1+\tan ^2x=\sec ^2x`

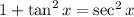
Then replace the denominator by sec^2 (x)

`(4\tan x)/(\sec ^2x)`

Since sec is the reciprocal of cos, then

`\sec ^2x=(1)/(\cos ^2x)`

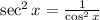
Replce sec^2(x) by 1/cos^2(x)

`(4\tan x)/((1)/(\cos ^2x))`

Since denominator of denominator will be a numerator

`4\tan x*\cos ^2x`

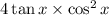
Use the value of tan

`\tan x=(\sin x)/(\cos x)`

Replace tan by sin/cos

`4*(\sin x)/(\cos x)*\cos ^2x`

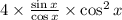
Reduce cos(x) up with cos(x) down

`\begin{gathered} 4*\sin x*\cos x= \\ 4\sin x\cos x \end{gathered}`

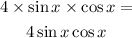
Use the identity

`\sin (2x)=2\sin x\cos x`
`4\sin x\cos x=2(2\sin x\cos x)`

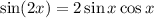
Replace 2 sin(x)cos(x) by sin(2x)

`2(2\sin x\cos x)=2\sin 2x`

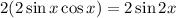
The answer is

2 sin(2x)