Given data:
* The mass of the crate is m = 64.3 kg.
* The height of the crate is h = 4.36 m.
Solution:
(a). The potential energy of the crate at the initial state is zero (as the height of the crate is zero at the initial state), thus, the change in the potential energy of the crate is,

where g is the acceleration due to gravity,
Substituting the known values,
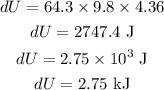
Thus, the change in the potential energy is 2.75 kJ.
(b). The work done to lift the crate is equal to the change in the potential energy of the crate.
Thus, the work done on the crate is 2.75 kJ.
(c). As the single is pulling the two ropes to increase the height of the crate, thus, the length of the rope pulled in terms of the height of the crate is,
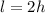
Substituting the known values,
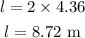
Thus, the length of the rope pulled to lift the crate is 8.72 meters.