Question

Divide the polynomial by the monomial (63xy^3+ 56x^2y^4)/(7xy)

Answer 1

9y² + 8xy³

Step-by-step explanation

To divide this polynomial by the given monomial, we can distribute the denominator into the sum,

`(63xy^3+56x^2y^4)/(7xy)=(63xy^3)/(7xy)+(56x^2y^4)/(7xy)`

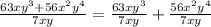
Then, each coefficient simplifies with the coefficient of the monomial, since both are multiples of 7. Also, in the first term, x cancels out, and we have to subtract 1 from the exponent of y. In the second term, we subtract 1 from both the exponents of x and y,

`(63xy^3)/(7xy)+(56x^2y^4)/(7xy)=9y^2+8xy^3`

Hence, the result is 9y² + 8xy³.