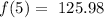Problem: consider the function f(x) whose second derivative is f' '(x)=4x+4sin(x). If f(0)=3 and f'(0)=4, what is f(5)?.
Solution:
Let the function f(x) whose second derivative is:
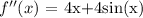
Now, the antiderivative (integral) of the above function would be:
EQUATION 1:
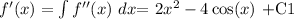
where C1 is a constant because we have an indefinite integral. Now the antiderivative (integral) of the above function f´(x) is:
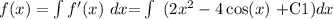
that is:
EQUATION 2:
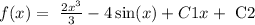
where C2 is a constant because we have an indefinite integral.
Now using the previous equation, if f(0)= 3 then:
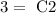
Now, using equation 1 and the fact that f ´(0) = 4, then we have:
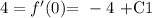
That is:
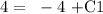
Solve for C1:
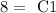
Now, replacing the constants C1 and C2 in equation 2, we have an expression for f(x):
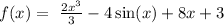
Then f(5) would be:
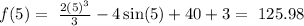
then the correct answer is: