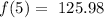Question

consider the function f(x) whose second derivative is f' '(x)=4x+4sin(x). If f(0)=3 and f'(0)=4, what is f(5)?

Answer 1

Problem: consider the function f(x) whose second derivative is f' '(x)=4x+4sin(x). If f(0)=3 and f'(0)=4, what is f(5)?​.

Solution:

Let the function f(x) whose second derivative is:

`f^(\prime\prime)(x)\text{ = 4x+4sin(x)}`

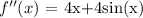
Now, the antiderivative (integral) of the above function would be:

EQUATION 1:

`f^(\prime)(x)=\int f^(\prime\prime)(x)\text{ }dx\text{= }2x^2-4\cos (x)\text{ +C1}`

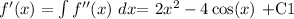
where C1 is a constant because we have an indefinite integral. Now the antiderivative (integral) of the above function f´(x) is:

`f(x)=\int f^(\prime)(x)\text{ }dx\text{=}\int \text{ (}2x^2-4\cos (x)\text{ +C1)}dx\text{ }`

that is:

EQUATION 2:

`f(x)=\text{ }(2x^3)/(3)-4\sin (x)+C1x+\text{ C2}`

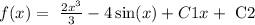
where C2 is a constant because we have an indefinite integral.

Now using the previous equation, if f(0)= 3 then:

`3=\text{ C2}`

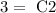
Now, using equation 1 and the fact that f ´(0) = 4, then we have:

`4=f^(\prime)(0)\text{= }^{}-4\text{ +C1}`

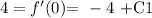
That is:

`4=\text{ }^{}-4\text{ +C1}`

Solve for C1:

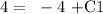
`8=\text{ }^{}\text{C1}`

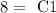
Now, replacing the constants C1 and C2 in equation 2, we have an expression for f(x):

`f(x)=\text{ }(2x^3)/(3)-4\sin (x)+8x+3`

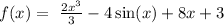
Then f(5) would be:

`f(5)=\text{ }(2(5)^3)/(3)-4\sin (5)+40+3=\text{ }125.98`

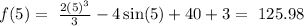
then the correct answer is:

`f(5)=\text{ }125.98`