Question

Finding a time to reach the limit in a word problem on exponential growth or decay

Answer 1

Step-by-step explanation

We are told that each year the value of the laptop is 75% of the value of the value of the previous year. This means that every year the current value of the laptop is multiplied by 0.75. Then if v is the original value of the laptop its value after t years is given by:

`V(t)=v0.75^t`

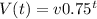
We need to find after which year V(t) is equal to 500 or less then we have V(t)≤500 and since the original value of the laptop was 4200 we have v=4200:

`4200*0.75^t\leq500`

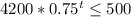
We divide both sides by 4200:

`\begin{gathered} (4200*0.75^t)/(4200)\leqslant(500)/(4200) \\ 0.75^t\leq(5)/(42) \end{gathered}`

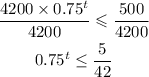
Then we apply the logarithm to both sides:

`\log_(10)(0.75^t)\leqslant\log_(10)((5)/(42))`

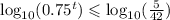
Then we use the property of logarithm regarding exponents:

And we divide both sides by the logarithm of 0.75 (we change the inequality symbol because log(0.75) is negative):

Then we get:

`t\ge7.398`

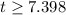
So the laptop's value is less than $500 after 7.398 years.

Answer

Since we are requested to write a whole number as the answer and the smallest whole number that is bigger than 7.398 is 8 we have that the answer is 8 years.