a. The point-slope equation is:

Where m is the slope and (x1,y1) are the coordinates of one point in the line. Also, you need to write the equation with inequalities, then you need to replace the = sign, for a <, > or <=, >= sign.
Let's start by finding the slope of the first set of points (9,7) (8,5).
The formula for the slope is:
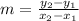
By replacing the values you obtain:
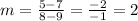
The slope is 2.
Now, replace this value into the slope-form equation and the values of the first point (9,7):
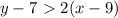
I choose the sign > (greater than), but you can choose anyone, the difference will be for the solution of the inequality. When you solve the inequality you will find that the x-values have to be greater than the solution you found, or less than... etc, it will depend on the sign you have in the inequality.
b. The slope-intercept equation is:

Where m is the slope and b the y-intercept.
Let's use the second set of points (2,9) and (2,7)
Start by calculating the slope:
![m=(7-9)/(2-2)=(-2)/(0)=\text{ undefined}]()
As there's no difference in the x-coordinates, the line is a vertical line at x=2.
Also, there's no y-intercept as the line never crosses the y-axis.
I will use the first set again, so you can understand the slope-intercept form.
From part a) you know that the slope is 2, let's replace it in the equation and use the first pair of coordinates to find b:
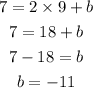
Thus, the slope-intercept with inequality will be:
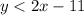
c. The standard form equation of a line is:
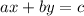
Let's use the third set of points (3,5) (5,4).
Start by finding the slope:
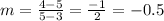
Now, you can start with the point-slope form and then convert it into the standard form:
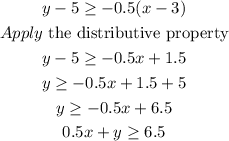
Where a=0.5, b=1 and c=6.5