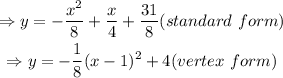Solution:
Given:
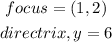
Step 1:
The equation of a parabola is given below as
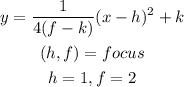
Step 2:
The distance from the focus to the vertex is equal to the distance from the vertex to the directrix:

Step 3:
Substitute the values in the general equation of a parabola, we will have
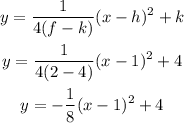
By expanding, we will have
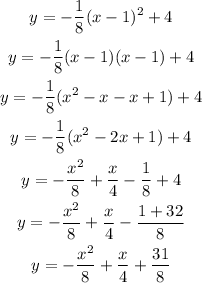
Hence,
The final answer is