Question

A park in a subdivision is triangular shaped. Two adjacent sides of the park are 533 feet and 525 feet. The angle between the sides is 53 degrees. To the nearest unit, what is the area of the park in square yards?A. 27,935B. 24,831C. 37,246D. 12,415thank you ! :)

Answer 1

Given:

Length of the two adjacent sides = 533 feet and 525 feet

Angle between the two sides = 53 degrees

Let's find the area of park.

Let's make a sketch representing this situation:

Let's first find the length of the third side.

Apply the cosine rule.

We have:

`\begin{gathered} a=√(533^2+525^2-2(533)(525)cos53) \\ \\ a=√(284089+275625-336805.7777) \\ \\ a=√(222908.2223) \\ \\ a=472.13\text{ ft} \end{gathered}`

Now, apply the Heron's formula to find the area:

`A=√(s(s-a)(s-b)(s-c))`

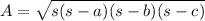
Where:

a = 472.13

b = 533

c = 525

Let's solve for s:

`\begin{gathered} s=(472.13+533+525)/(2) \\ \\ s=(1530.13)/(2) \\ \\ s=765.1\text{ } \end{gathered}`

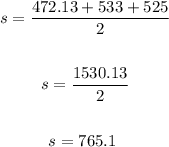
• Therefore, the area will be:

`\begin{gathered} A=√(765.1(765.1-472.13)(765.2-533)(765.1-525)) \\ \\ A=√(765.1(292.97)(232.1)(240.1)) \\ \\ A=111738.81\text{ ft}^2 \end{gathered}`

The area in square feet is 111,738.81 square feet.

Now, let's find the area in square yards.

Apply the metrics of measurement.

Where:

1 square yard = 9 square feet

Thus, we have:

111,738.81 square feet =

`(111738.81)/(9)=12415.4\approx12415\text{ square yards}`

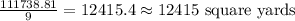
Therefore, the area of the park in square yards is 12,415 square yards.

ANSWER:

12,415 square yards.