Given:
Length of the two adjacent sides = 533 feet and 525 feet
Angle between the two sides = 53 degrees
Let's find the area of park.
Let's make a sketch representing this situation:
Let's first find the length of the third side.
Apply the cosine rule.
We have:

Now, apply the Heron's formula to find the area:

Where:
a = 472.13
b = 533
c = 525
Let's solve for s:
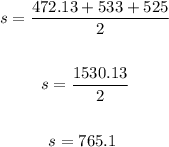
• Therefore, the area will be:

The area in square feet is 111,738.81 square feet.
Now, let's find the area in square yards.
Apply the metrics of measurement.
Where:
1 square yard = 9 square feet
Thus, we have:
111,738.81 square feet =

Therefore, the area of the park in square yards is 12,415 square yards.
ANSWER:
12,415 square yards.