Question

A gumball machine contains orange, yellow, and purple gum balls. The probability of getting an orange gumball is 3/4. The probability of getting a yellow gumball is 1/6. If there are 36 gumballs in the machine, how many are there of each color number of purple marbles _______ number of yellow marbles_____ number of orange marbles______

Answer 1

Given:

Probability of getting orange gumball is, p(o) = 3/4.

Probability of getting yellow gumball is, p(y) = 1/6.

The objective is to find the number of each colored gumballs.

Since, the sum of the events of probability is always 1.

Then, the probability of purple ball p(p) can be calculated as,

`\begin{gathered} (3)/(4)+(1)/(6)+p(p)=1 \\ p(p)=1-(3)/(4)-(1)/(6) \\ p(p)=(12-3(3)-1(2))/(12) \\ p(p)=(1)/(12) \end{gathered}`

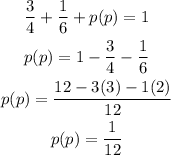
Since, it is given that the total number of gumball is N = 36.

Then, the number of orange ball can be calculated as,

`\begin{gathered} p(o)=(n(o))/(N) \\ (3)/(4)=(n(o))/(36) \\ n(o)=36\cdot(3)/(4) \\ n(o)=27\text{ balls.} \end{gathered}`

Similarly, the number of yellow ball can be calculated as,

`\begin{gathered} p(y)=(n(y))/(N) \\ (1)/(6)=(n(y))/(36) \\ n(y)=(36)/(6) \\ n(y)=6 \end{gathered}`

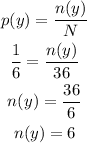
And the number of purple ball can be calculated as,

`\begin{gathered} p(p)=\frac{n(p)_{}}{N} \\ (1)/(12)=(n(p))/(36) \\ n(p)=(36)/(12) \\ n(p)=3 \end{gathered}`

Hence, the number of orange ball is 27, number yellow ball is 6 and number of purple ball is 3.