Answer:
2 hours
Step-by-step explanation:
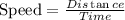
The first bicyclist rides at a speed of 8 mph. Therefore:
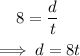
One hour later, the second bicyclist leaves and rides at a speed of 12 mph.
Therefore, the time of the second bicyclist = (t-1) hours.
Therefore:
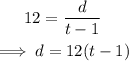
Since the second bicyclist will catch up to the first bicyclist, the distance traveled will be the same.
So:
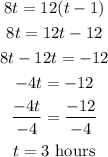
Therefore, the second bicyclist will have traveled for:
(t-1) = (3-1) =2 hours.