Question

24) A 0.042-kg pet lab mouse sits on a 0.35 kg air-track cart. The cart is at rest, as is a second cart with a mass of 0.25 kg. The lab mouse now jumps to the second cart. After the jump, the 0.35-kg cart has a speed of u1=0.88m/s. What is the speed v2 of the mouse and the 0.25-kg cart? |

Answer 1

The mass of the mouse, m₁=0.042 kg

The mass of the 1st cart, m₂=0.35 kg

The mass of the second cart, m₃=0.25 kg

The speed of the 1st car after the jump, u₁=0.88 m/s

From the law of conservation of momentum, the momentum of a system should always remain the same.

Before the mouse jumps from one cart to another, all the objects were at rest. Therefore the total momentum of the system was zero.

Thus after the mouse jumps, the total momentum of the system should be equal to zero.

Thus the momentum of the second cart and the mouse will be equal in magnitude to the momentum of the first cart but it will be in the opposite direction.

Thus,

`m_2u_1=(m_1+m_3)v_2`

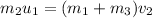
On substituting the known values,

`\begin{gathered} 0.35*0.88=(0.042+0.25)v_2 \\ \Rightarrow v_2=(0.35*0.88)/((0.042+0.25)) \\ =1.05\text{ m/s} \end{gathered}`

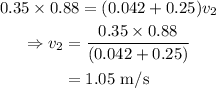
Thus the speed of the mouse and the second cart after the mouse jumps is 1.05 m/s