Question

The seventh term of a geometric sequence is 1/4 The common ratio 1/2 is What is the first term of the sequence?

Answer 1

16

Step-by-step explanation:

The equation for the term number n on a geometric sequence can be calculated as:

`a_n=a_{}\cdot r^(n-1)`

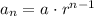
Where r is the common ratio and a is the first term of the sequence.

So, if the seventh term of the sequence is 1/4 we can replace n by 7, r by 1/2, and aₙ by 1/4 to get:

`(1)/(4)=a\cdot((1)/(2))^(7-1)`

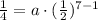
Then, solving for a, we get:

`\begin{gathered} (1)/(4)=a((1)/(2))^6 \\ (1)/(4)=a((1)/(64)) \\ (1)/(4)\cdot64=a\cdot(1)/(64)\cdot64 \\ 16=a \end{gathered}`

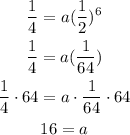
So, the first term of the sequence is 16.