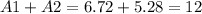For each triangle identify a base and corresponding height use them to find the are

Question

asked Dec 28, 2023 4.1k views

1 Answer

Chase Ries · Answer 1 · 2024-01-02T13:01:13+0000

A)

For this tringle we can turn the figure like this:

now we have two right triangles and we can calulate the base of the first triangle with the sin law

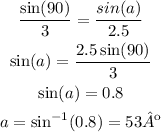
$\begin{gathered} (\sin (90))/(3)=(sin(a))/(2.5) \\ \sin (a)=(2.5\sin (90))/(3) \\ \sin (a)=0.8 \\ a=\sin ^(-1)(0.8)=53º \end{gathered}$

the angle b is going to be:

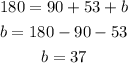
$\begin{gathered} 180=90+53+b \\ b=180-90-53 \\ b=37 \end{gathered}$

Now the base is going to be:

$\begin{gathered} (\sin(90))/(3)=\frac{\sin(37)}{\text{base}} \\ \text{base}=(3\sin (37))/(\sin (90))=1.8 \end{gathered}$

and the base of the secon triangle is going to be:

$\text{base}2=7.2-1.8=5.4$

And the area of the triangles is going to be:

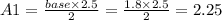
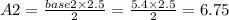
so in total the area is going to be:

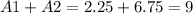
B)

the procedure is similar, first we turn the tiangle like this:

the angle a is going to be:

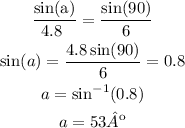
$\begin{gathered} \frac{\text{sin(a)}}{4.8\text{ }}=(\sin (90))/(6) \\ \sin (a)=(4.8\sin (90))/(6)=0.8 \\ a=\sin ^(-1)(0.8) \\ a=53º \end{gathered}$

the angle b is going to be:

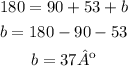
$\begin{gathered} 180=90+53+b \\ b=180-90-53 \\ b=37º \end{gathered}$

now the base is going to be:

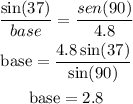
$\begin{gathered} (\sin (37))/(base)=(sen(90))/(4.8) \\ \text{base}=(4.8\sin (37))/(\sin (90)) \\ \text{base}=2.8 \end{gathered}$

and the base of the other triangle will be:

$\text{base}2=5-2.8=2.2$

And the area of the triangles will be:

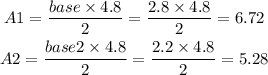
$\begin{gathered} A1=(base*4.8)/(2)=(2.8*4.8)/(2)=6.72 \\ A2=(base2*4.8)/(2)=(2.2*4.8)/(2)=5.28 \end{gathered}$

And the total area will be: