1 Answer

Aun Shahbaz Awan · Answer 1 · 2023-06-07T12:34:18+0000

The triangle ABC is an equilateral triangle. This means that each angle equals 60°. Hence, the angle at B is 60°.

The length of each side of ABC is given to be 3 cm long.

We can get the length of side AD by solving the triangle ABD using the Cosine Rule given to be:

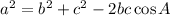
$a^2=b^2+c^2-2bc\cos A$

Since we're considering triangle ABD, and we have the measure of angle B, we can use the relationship:

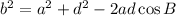
$b^2=a^2+d^2-2ad\cos B$

Note that a, b, and d are the sides, such that:

$\begin{gathered} a=BD=BC+CD=3+4=7\operatorname{cm} \\ b=AD \\ d=AB=3\operatorname{cm} \end{gathered}$

Substituting these values, we have:

$\begin{gathered} AD^2=7^2+3^2-2(7*3*\cos 60) \\ AD^2=49+9-42\cos 60 \\ AD^2=37 \\ AD=\sqrt[]{37} \\ AD=6.08\operatorname{cm} \end{gathered}$

The length of AD is 6.08 cm to 2 decimal places.

Please log in or register to add a comment.