Question

Determine weather it is a function, and state it’s domain and range.

Answer 1

Find the inverse of:

`f(x)=(3x-24)^2`

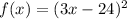
The variable x can take any real value and the function f(x) exists. This means

the domain of f(x) is (-∞, +∞).

Now find the inverse function.

`\begin{gathered} y=(3x-24)^2 \\ \pm\sqrt[]{y}=3x-24 \\ \pm\sqrt[]{y}+24=3x \\ x=\frac{\pm\sqrt[]{y}+24}{3} \\ x=\pm(1)/(3)\sqrt[]{y}+8 \end{gathered}`

Swapping letters, we get the inverse function:

`y=\pm(1)/(3)\sqrt[]{x}+8`

For each value of x, we get two values of y, thus this is not a function.

The domain of the inverse is restricted to values of x that make the square root exist, thus the domain is x ≥ 0, or [0, +∞)

The range of the inverse is the domain of the original function, that is, (-∞, +∞)

Function: No

Domain: [0, +∞)

Range: (-∞, +∞)

The choice to select is shown below.