Question

Personal finance Funding a retirement goal. Austin Miller wishes to have $800,000 in a retirement fund 20 years from now. He can create the retirement fund by making a single lump-sum deposit today.   How much would Austin need to have on deposit at retirement in order to withdraw $35,000 annually over the 15 years if the retirement fund earns 4 percent?   To achieve his annual withdrawal goal of $35,000 calculated in part b, how much more than the amount calculated in part a must Austin deposit today in an investment earning 4 percent annual interest?

Answer 1

$389,200

$21,200

Since,

`\text{PMT}=\frac{PV}{\text{PVA}}`

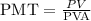
We are to find PV when the PMT is $35000. Since the PVA is 11.12,

`PV=\text{PVA}\cdot\text{PMT}`
`PV=(11.12)(35000)=389200`

Hence, Austin would need to deposit $389,200.

For the last part, we first need to solve the PV at 4% in 20 years.

The PVIF would be:

`\text{PVIF}=(1)/((1+0.04)^(20))=0.46`

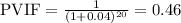
Then, solving for the PV:

`PV=800000(0.46)=368000`

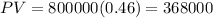
Now, to know how much more should Austin deposit, we need to subtract the original PV from the PV that we got from part B.

That would be,

`389200-368000=21200`

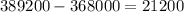
Austin would need to deposit $21,200 more to achieve his withdrawal goal.