The percentage of alcohol of a solution i is given by the quotient:
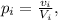
where v_i is the volume of alcohol in the solution i and V_i is the volume of the solution i.
From the statement of the problem we know that:
1) Solution A has 10% of alcohol, i.e.
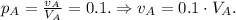
2) Solution B has 60% of alcohol, i.e.
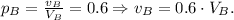
3) The volume of solution A is V_A = 200ml.
4) The resulting mixture must have a percentage of 40% of alcohol, so we have that:
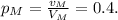
5) The volume of the mixture v_M is equal to the sum of the volumes of alcohol in each solution:
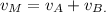
6) The volume of the mixtureVv_M is equal to the sum of the volumes of each solution:
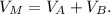
7) Replacing 5) and 6) in 4) we have:
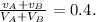
8) Replacing 1) and 2) in 7) we have:
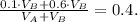
9) Replacing 3) in 8) we have:
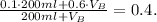
Now we solve the last equation for V_B:
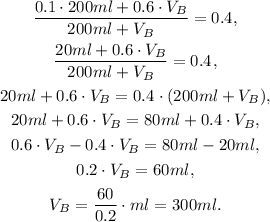
We must use 300ml of Solution B to have a 40% alcohol solution as the resulting mixture.
Answer: 300ml of Solution B.