Question

Identify the leading coefficient, degree and end behavior. write the number of the LC and degree

Answer 1

Given

`P(x)=-4x^4-3x^3+x^2+4`

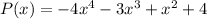
Solution

The LC is -4

End behavior is determined by the degree of the polynomial and the leading coefficient (LC).

TThe degree of this polynomial is the greatest exponent is

`\begin{gathered} x\rightarrow\infty\text{ then P\lparen x\rparen} \\ p(\infty)=-4(\infty)^4-3(\infty)^3+\infty^2+4 \\ p(\infty)=-4\infty^4-3\infty^3+\infty^2+4 \\ P(\infty)=-\infty \\ \end{gathered}`
`\begin{gathered} x\rightarrow-\infty \\ p(-\infty)=-4(-\infty)^4-3(-\infty)^3+(-\infty)^2+4 \\ P(-\infty)=-4\infty^4+3\infty^3+\infty^2+4 \\ P(-\infty)=-\infty \end{gathered}`

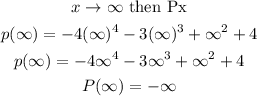
The degree is even and the leading coefficient is negative.

The final answer