Question

Solving triangles using the law of cosines . Find m

Answer 1

The law of cosines is defined as follows:

`a^2=b^2+c^2-2bc\cos A`

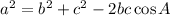
For the given triangle

a=AC=8

b=AB=14

c=BC=11

∠A=∠B=?

-Replace the lengths of the sides on the expression

`8^2=14^2+11^2-2\cdot14\cdot11\cdot\cos B`

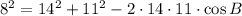
-Solve the exponents and the multiplication

`\begin{gathered} 64=196+121-308\cos B \\ 64=317-308\cos B \end{gathered}`

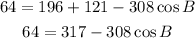
-Pass 317 to the left side of the expression by applying the opposite operation to both sides of it

`\begin{gathered} 64-317=317-317-308\cos B \\ -253=-308\cos B \end{gathered}`

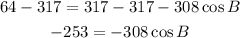
-Divide both sides by -308

`\begin{gathered} -(253)/(-308)=-(308\cos B)/(-308) \\ (23)/(28)=\cos B \end{gathered}`

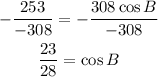
-Apply the inverse cosine to both sides of the expression to determine the measure of ∠B

`\begin{gathered} \cos ^(-1)(23)/(28)=\cos ^(-1)(\cos B) \\ 34.77º=B \end{gathered}`

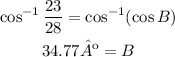
The measure of ∠B is 34.77º