The law of cosines is defined as follows:
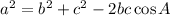
For the given triangle
a=AC=8
b=AB=14
c=BC=11
∠A=∠B=?
-Replace the lengths of the sides on the expression
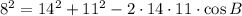
-Solve the exponents and the multiplication
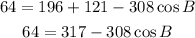
-Pass 317 to the left side of the expression by applying the opposite operation to both sides of it
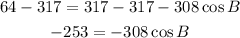
-Divide both sides by -308
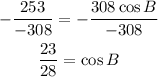
-Apply the inverse cosine to both sides of the expression to determine the measure of ∠B
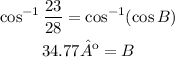
The measure of ∠B is 34.77º