Given:
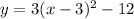
The quadractic equation above is written in vertex form:

Where:
(h, k) is the coordinate of the vertex of the parabola
We have
a = 3
h = 3
k = -12
Let's find the following:
A.) Identify the coefficients, a, h, and k
Comparing the equation with the vertex form, we have:
a = 3
h = 3
k = -12
B.) Identify whether the graph opens up or opens down.
If a is greater than zero, then the graph opens up
If a is less than zero, then the graph opens downwards
Here, a = 3
Since a is greater than zero, the graph opens up.
The graph of the equation opens up
C.) Find the vertex.
The coordinates of the vertex is = (h, k)
Given:
h = 3
k = -12
Therefore, the vertex is: (3, -12)
D.) Find the axis of symmetry.
The axis of symmetry is the line that passes through the vertex and the focus.
To find the axis of symmetry we have:
x = h
where h = 3
Thus, the axis of symmetry is:
x = 3
E.) Let's find two more points.
Point 1 ==> (x, y)
Let's take x = 1
Substitute 1 for x and solve for y:
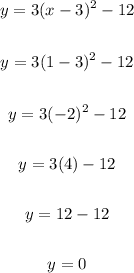
When x is 1, y is 0.
Therefore, we have the point:
(x, y) ==> (1, 0)
Point 2:
Let's take x = 2
Substitute 2 for x and solve for y:
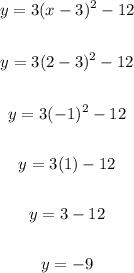
When x is 2, y is -9.
Therefore, we have the points:
(x, y) ==> (2, -9)
ANSWER:
A.) a = 3
h = 3
k = -12
B.) The graph opens up
C.) (3, -12)
D.) x= 3
E.) (1, 0), (2, -9)