Question

Find the magnitude of the sumof these two vectors:B63.5 m101 m57.0°

Answer 1

Vector diagram:

The resultant vector is given as,

`R=\sqrt[]{A^2+B^2+2AB\cos \theta}`

Here, θ is the angle between vector A and B.

Substituting all known values,

`\begin{gathered} R=\sqrt[]{(63.5)^2+(101)^2+2*101*63.5*\cos (33^(\circ))} \\ =158.08\text{ m} \end{gathered}`

Therefore, the resultant magnitue of the sum of these two vectors are 158.08 m.

The x-component of the magnitude is given as,

`\begin{gathered} R_x=101\cos (57^(\circ))+63.5\cos (90^(\circ)) \\ =55.0\text{ m} \end{gathered}`

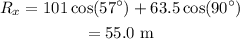
The y- component of the magnitude is given as,

`\begin{gathered} R_y=63.5\sin (90^(\circ))+101\sin (57^(\circ)) \\ =148.2\text{ m} \end{gathered}`

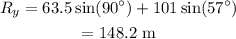
Therefore, the direction is given as,

`\begin{gathered} \phi=\tan ^(-1)((R_y)/(R_x)) \\ =\tan ^(-1)(\frac{148.2\text{ m}}{55.0\text{ m}}) \\ =69.63^(\circ) \end{gathered}`

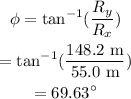
Therefore, the direction of the resultant vector is 69.63°.