Vector diagram:
The resultant vector is given as,
![R=\sqrt[]{A^2+B^2+2AB\cos \theta}](https://img.qammunity.org/2023/formulas/physics/college/p9yv3cn0vcn295cj6gehq5gy50m1h498dt.png)
Here, θ is the angle between vector A and B.
Substituting all known values,
![\begin{gathered} R=\sqrt[]{(63.5)^2+(101)^2+2*101*63.5*\cos (33^(\circ))} \\ =158.08\text{ m} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/yyhanb72c8g9jlf7037anixahaimewtwxw.png)
Therefore, the resultant magnitue of the sum of these two vectors are 158.08 m.
The x-component of the magnitude is given as,

The y- component of the magnitude is given as,
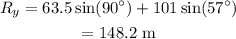
Therefore, the direction is given as,
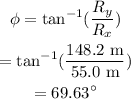
Therefore, the direction of the resultant vector is 69.63°.