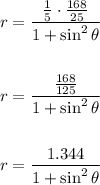In order to find the polar equation of the ellipse, first let's find the rectangular equation.
Since the directrix is a vertical line, the ellipse is horizontal, and the model equation is:
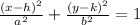
Where the center is located at (h, k), the directrix is x = -a/e and the eccentricity is e = c/a.
So, if the eccentricity is e = 1/5 and the directrix is x = -7, we have:

Now, let's calculate the value of b with the formula below:
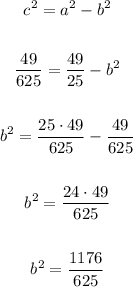
Assuming h = 0 and k = 0, the rectangular equation is:
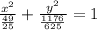
Now, to convert to polar form, we can do the following steps:
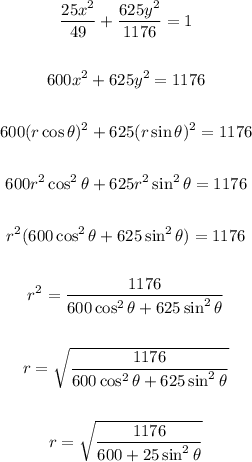
Another way of writing this equation in polar form is:
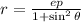
Where p is the distance between the focus and the directrix.
Since the foci are located at (±c, 0) = (±7/25, 0) and the directrix is x = -7, the distance is:
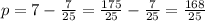
So the equation is: