Let's begin by listing out the given information:
A fair dice has 6 sides
The dice has its sides numbered from 1-6
The number of sides with even numbers (2, 4 & 6) equals 3
The number of sides with odd numbers (1, 3 & 5) equals 3
The probability of rolling an even number is given as shown below:
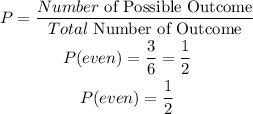
The probability of rolling an odd number is given as shown below:
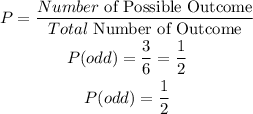
The probability of rolling an even number followed by an odd number is obtained by the product of the probabilities above. We have:
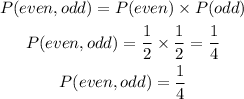
Therefore, the probability of rolling an even number and then an odd number is 1/4