Question

Refer to the rectangle ABCD, shown below, where m(<4)=10degrees. Need help.

Answer 1

From the statement of the problem, we know that:

`m(\angle4)=18^(\circ)\text{.}`

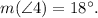
From the diagram, we see that:

1) ∠1 and ∠4 are complementary angles, so they sum up 90°:

`\begin{gathered} m\mleft(\angle1\mright)+m\mleft(\angle4\mright)=90\degree \\ m\mleft(\angle1\mright)=90\degree-m\mleft(\angle4\mright), \\ m(\angle1)=90\degree-18^(\circ)=72^(\circ)\text{.} \end{gathered}`

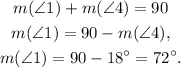
2) ∠4, ∠3 and a right angle are inner angles of a triangle, so they must sump up 180°:

`\begin{gathered} m(\angle4)+m(\angle3)+90^(\circ)=180^(\circ)\text{.} \\ m(\angle3)=180^(\circ)-90^(\circ)-m(\angle4), \\ m(\angle3)=180^(\circ)-90^(\circ)-18^(\circ)=72^(\circ)\text{.} \end{gathered}`

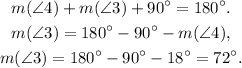
3) ∠3 and ∠2 are complementary angles, so they sum up 90°:

`\begin{gathered} m(\angle3)+m(\angle2)=90^(\circ), \\ m(\angle2)=90^(\circ)-m(\angle3), \\ m(\angle2)=90^(\circ)-72^(\circ)=18^(\circ)\text{.} \end{gathered}`

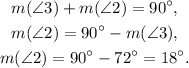
Answer

c. m(∠1) = 72°, m(∠2) = 18°, m(∠3) = 72°.