From the statement of the problem, we know that:
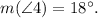
From the diagram, we see that:
1) ∠1 and ∠4 are complementary angles, so they sum up 90°:
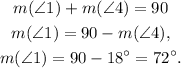
2) ∠4, ∠3 and a right angle are inner angles of a triangle, so they must sump up 180°:
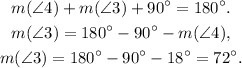
3) ∠3 and ∠2 are complementary angles, so they sum up 90°:
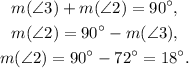
Answer
c. m(∠1) = 72°, m(∠2) = 18°, m(∠3) = 72°.